 |
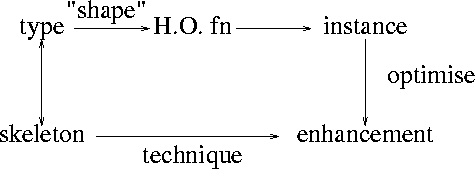
The previous work of the authors sketched above can be seen as taking two different roads for program development starting from the same place (a type definition) and arriving at the same destination (the enhanced program), as shown in Figure 1.
Sterling suggested the low road in Figure 1, going from the type to the enhancement via the skeleton. To explain how to travel the low road is simple and does not require very abstract thinking or complex software tools. Such an approach to systematic program construction may be favoured by many programmers.
Naish suggested the high road in Figure 1, writing a version of
foldr for
the given type, using an instance of this foldr
(a particular call to it)
and then optimising, for example using
a partial evaluator. The additional abstraction and concentration on
semantics rather than syntax may be favoured by more experienced
programmers using more advanced programming environments.
The work on shape allows us to automatically obtain the foldr
definition from the definition of the type.
There is a very simple mapping between algebraic types and a class of logic
programs called RUL programs (Yardeni and Shapiro, [YS90]).
RUL programs only
have unary predicates. The argument of each clause head has the top level
functor instantiated but all sub-terms are unique variables. Clause heads
are mutually non-unifiable (thus predicates are deterministic when their
arguments are instantiated). The arguments of all calls are variables which
occur in the head and nowhere else in the body. Examples of RUL programs
are is_list/1 (Program 1) and is_tree/1 (Program 2a).
The high road taken by functional programmers is equivalent to starting with a skeleton which is a RUL program and enhancing it with predicates which behave as functions, that is, they are deterministic and always succeed. The theory of functional programming can be used to prove results concerning composition of enhancements, for example, and generally give a theoretical justification for the idea of enhancement.