Model-theoretic semantics

We first define interpretations and models then discuss the motivation for these definitions and the properties of models.

Definition 2   An interpretation is a mapping from ground atoms to the truth values true, false and inadmissible. The interpretation of $= / 2$ is restricted to be (two-valued) syntactic equality.

Conjunction and disjunction are defined as below -- the same as in Kleene's strong three-valued logic [KleeneKleene1952]:

$\wedge$	T	F	I
T	T	F	I
F	F	F	F
I	I	F	I

$\vee$	T	F	I
T	T	T	T
F	T	F	I
I	T	I	I

Definition 3 (model of $P$)   An interpretation is a model of a disjunctive definite program $P$ if no instance of a clause in $P$ is mapped (by the interpretation and definitions of conjunction and disjunction) to $\textbf{F} \leftarrow \textbf{T}$ or $\textbf{F} \leftarrow \textbf{I}$.

That is, if the head is F, the body is F. Note that the traditional two-valued model theory is a special case of these definitions where the set of inadmissible atoms is empty. This definition of a model can be seen as giving a two-valued interpretation to an implication connective. It differs from Kleene's (weak and strong) logics, in which implications can have all three values. In [PrzymusinskiPrzymusinski1989], and [Apt and BolApt and Bol1994], an alternative definition of a model is given -- we refer to these as strong models:

Definition 4 (strong model of $P$)   An interpretation is a strong model of a disjunctive definite program $P$ if it is a model of $P$ and no instance of a clause in $P$ is mapped to $\textbf{I} \leftarrow \textbf{T}$.

Strong models significantly restrict intended interpretations and/or programming style. For example, they do not allow interpretations where instances of facts in the program are inadmissible. Our interpretation of merge/3 is not a strong model due to clause instances such as merge([],a,a). To make our intended interpretation a strong model of the first clause a test such as sorted_list(Bs) would have to be added. We have attempted to make our definition of a model as weak as possible: it just avoids the two classes of bugs discussed earlier. The definitions of conjunction and disjunction follow the same principle.

For conjunction, the key question is whether $\textbf{I} \wedge \textbf{F}$ should equal $\textbf{I}$ or $\textbf{F}$. A choice of $\textbf{I}$ would be similar to strict type schemes in which a conjunction containing an ill-typed atom is ill-typed, whether it succeeds or fails. Programs are restricted so that all derivations are well typed, not just successful ones (distinguishing between these two cases cannot be done statically). The choice of $\textbf{F}$ is similar to less restrictive type schemes which only restrict successful derivations; this is discussed further in [NaishNaish1992b]. It allows runtime checking of types (or other assertions) to be supported. The body of a clause instance can have checks which fail (have truth value $\textbf{F}$) as well as inadmissible calls, that is, the clause is of the form $\textbf{F} \leftarrow \textbf{F} \wedge \textbf{I}$. This would not be acceptable with the stricter definition of conjunction.

For disjunction, the key question is whether $\textbf{I} \vee \textbf{T}$ should equal $\textbf{I}$ or $\textbf{T}$. In strict type schemes a disjunction containing an ill-typed atom is ill-typed even if a well-typed disjunct succeeds. Even in the less strict scheme of [NaishNaish1992b] disjunctions must be implemented as separate clauses and each clause must be ``type correct''. This is the reason we introduced disjunctive clauses: by choosing $\textbf{T}$ we can have a less restrictive condition.

The structure of the set of all models is more complex than in the two-valued case. There are several model intersection properties of interest. The first relates models with the same set of inadmissible atoms:

This proposition also holds for strong models. It generalises the two-valued model intersection property (where $I$ is the empty set, $\phi$). If there are two models with no true atoms then a similar result holds for the intersection of sets of inadmissible atoms. This is generalised in the following proposition (which does not hold for strong models).

Models exist with no inadmissible atoms (for example, all atoms are true) and with no true atoms (for example, all atoms are inadmissible), so from the two propositions above it follows that a least model (with respect to $T$) of the form $\langle \phi,T\rangle$ exists and a least model (with respect to $I$) of the form $\langle I,\phi\rangle$ exists. These two models have the same set of false atoms (just the role of true and inadmissible are swapped). These models are equivalent to the least two-valued model of the program.

If the set of false atoms is the same in two models, either the true atoms or inadmissible atoms can be intersected and the result is a model. In fact, any partitioning of the true and inadmissible atoms is a model:

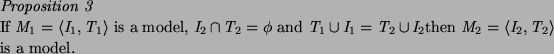
Thus we have a set of (at least two) minimal models (with respect to $T$/$I$), all with the same set of false atoms (the false atoms of the least two-valued model).

This result is essentially the reason why treating inadmissible atoms as true results in correct declarative diagnosis of wrong answers. For models of the completion this result does not hold.

There is another natural partial ordering of three-valued interpretations known as the information ordering (we treat the third truth value as ``don't care'', but in some contexts ``don't know'' is appropriate).

Definition 5 (information ordering, $\subseteq_i$)   Given two interpretations, $M_1$ and $M_2$, $M_1 \subseteq_i M_2$ if $T_1 \subseteq T_2 \wedge F_1 \subseteq F_2$, where $T_1$ ($F_1$) and $T_2$ ($F_2$) are the true (false) atoms in $M_1$ and $M_2$, respectively.

The $\subseteq_i$-least model has all atoms inadmissible. The $\subseteq_i$-least strong model has the least two-valued model as the true atoms and all other atoms inadmissible, the same as the $I$-least model with $I$ and $F$ swapped. Atoms in the least two-valued model are true in all strong models.