Relationships between semantics

Next: A semantics for normal Up: A semantics for definite Previous: Fixpoint semantics

Relationships between semantics

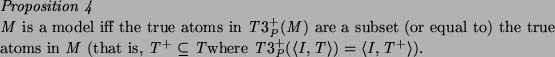
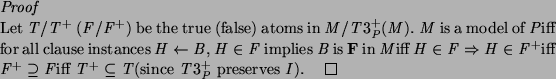
The relationship between three-valued models and / $T3^{+}_P$ is similar to the relationship between two-valued models and :
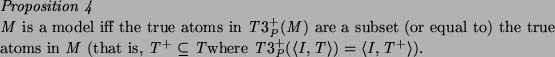
$\begin{proposition} $M$\ is a model iff the true atoms in $T3^{+}_P(M)$\ are a s... ...re $T3^{+}_P(\langle I, T\rangle) = \langle I, T^{+}\rangle$). \end{proposition}$

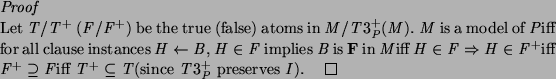
$\begin{proof} \par Let $T/T^{+}$\ ($F/F^{+}$) be the true (false) atoms in $M/T3... ...supseteq F$iff $T^{+} \subseteq T$(since $T3^{+}_P$\ preserves $I$). \end{proof}$

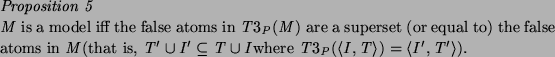
$\begin{proposition} $M$\ is a model iff the false atoms in $T3_P(M)$\ are a supe... ... I$where $T3_P(\langle I, T\rangle) = \langle I', T'\rangle$). \end{proposition}$

$\begin{proof} As above (change $T3^{+}_P$\ to $T3_P$\ and skip the last step). \end{proof}$

The relationship between least fixpoints, minimal models and success set is more complex than the two-valued case since there are multiple partial orders of interest and multiple minimal models by some measures. However, nearly all minimal models we have considered bear strong relationships with the success set (the least fixpoint of and least two-valued model). The union of true and inadmissible atoms in models which minimise or (or $I \cup T$ ) is . These models are least fixpoints of $T3^{+}_P$ where is fixed to a suitable value (such as $\phi$ or ). For $\subseteq_i$ the minimum strong model has as the true atoms and this is the least fixpoint of .

The main theorem we have concerns soundness for admissible atoms. A successful atom may not be true, since inadmissible atoms can succeed. However, an admissible atom which succeeds must be true if the intended interpretation is a model.

$\begin{theorem}[Soundness for admissible atoms] If $\langle I,T\rangle $\ is a model, $A$\ is admissible and $A \in SS$\ then $A \in T$. \end{theorem}$

$\begin{proof} $I \cup T \supseteq SS$\ by the propositions above. The result follows. \end{proof}$

A form of completeness is inherited from the two-valued case:
$\begin{theorem} If $A$\ is true or inadmissible in every model then $A \in SS$. \end{theorem}$

$\begin{proof} If $A$\ is not false in any three-valued model it is not false in ... ... models), so it is true in every two-valued model and hence in $SS$. \end{proof}$

This result is not really useful in practice for several reasons, which we discuss in Section 5.4.

Next: A semantics for normal Up: A semantics for definite Previous: Fixpoint semantics

2005-08-02