


Next: Model-theoretic semantics
Up: A semantics for normal
Previous: A semantics for normal
The operational semantics we use is essentially SLDNF resolution,
where negative literals must be ground in order to be selected.
We define trees to formalise the operational semantics. There are a
few differences between our definitions and the standard SLDNF tree
definitions. First, for technical convenience evaluation of negative
literals is done within the same tree structure (like [Martelli and TricomiMartelli and
Tricomi1992],
rather than having separate trees of different ranks) and equality
atoms/constraints are used rather than substitutions. Second, treatment
of floundering within negation is improved (it is often done poorly).
Third, we distinguish between searching for all solutions and just some
solution(s). Our main aim is to establish results about observables from
Prolog computations, namely, zero or more (possibly floundered) computed
answers and possibly an indication there are no (more) answers (we ignore
computations which are aborted -- we have no results for such cases).
These are always the result of a finite search and we define finite
trees which correspond to such computations. Even if all SLDNF trees
are infinite the search may be finite because only some solution(s)
may be needed (at the top level or inside a negation).
Definition 9 (SLDDNF tree)
An SLDDNF tree is a (possibly infinite) tree where nodes are connected
by positive or negative edges. The positive nodes of a (sub)tree are
those connected to the root with a sequence of positive edges.
Each node contains a conjunction of literals including equality atoms.
Nodes containing an unsatisfiable set of equality atoms are said to be
failed and have no children. Nodes containing a satisfiable set
of equality atoms and no other literals are said to be successful
and have no children. A literal is said to be grounded if the
substitution obtained by unifying the arguments of each equality atom
would make the literal ground. Nodes containing only a satisfiable
set of equality atoms and non-grounded negative literals are said
to be floundered and have no children. Other nodes have a
selected literal, which is not an equality atom and must be
grounded if it is negative.
If the goal in node 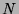 is
is
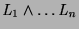 and the selected
literal is
and the selected
literal is 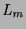 , then
, then
- If
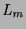 is an atom
is an atom 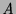 and
and
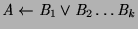 is a head instance of its definition, then
is a head instance of its definition, then 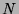 has
has 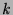 children,
connected with positive edges, with goals
children,
connected with positive edges, with goals
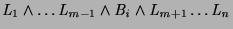 , for
, for
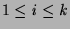 .
.
- If
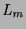 is a negative literal
is a negative literal 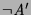 , there is one child
connected with a negative edge, containing goal
, there is one child
connected with a negative edge, containing goal 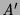 and the equality
atoms from
and the equality
atoms from 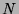 . If the subtree for
. If the subtree for 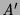 has a positive successful node
then
has a positive successful node
then 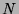 has a child, connected with a positive edge, which is failed.
If the subtree for
has a child, connected with a positive edge, which is failed.
If the subtree for 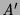 is finite and all positive leaves are failed,
then
is finite and all positive leaves are failed,
then 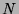 has a child, connected with a positive edge, which contains
has a child, connected with a positive edge, which contains
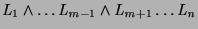 . If the subtree for
. If the subtree for 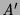 is finite, there are no positive successful nodes but there is a positive
floundered node, then
is finite, there are no positive successful nodes but there is a positive
floundered node, then 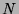 has a child, connected with a positive edge,
which is identical to
has a child, connected with a positive edge,
which is identical to 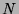 . Otherwise (the negative subtree is infinite
with no successful nodes),
. Otherwise (the negative subtree is infinite
with no successful nodes), 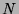 has no positive children and is considered
a positive leaf.
has no positive children and is considered
a positive leaf.
Definition 11 (All-observations tree)
An (SLDDNF) all-observations tree is an observations subtree of
SLDDNF tree
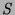
which includes all positive nodes of
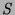
.
A Prolog implementation can be seen as searching an SLDDNF tree (typically
depth-first and left to right) for one or more successful positive nodes.
When such nodes are found at the top level the equations in the node
(equivalent to variable bindings) may be displayed in a suitable
fashion and the search may stop. When such nodes are found within a
negation the search typically stops and backtracking is initiated at
the higher level (where the negation was called). Observation trees
can model such behaviour. All-observations trees model computations
which find all solutions and terminate. Finitely failed observations
trees are all-observations trees (note that corresponding SLDDNF trees
may have infinite branches inside negations). We do not explicitly
model computations which flounder without succeeding or searching the
entire tree. They are of limited interest, especially inside negation,
though it would be easy to modify our definitions to support them.
Similarly, we do not model non-depth-first computations where some
branches are only partially searched.
Many implementations neglect to check that negative literals are ground
(leading to unsoundness), and even those which do typically have unsound
treatment of floundering within negation (this is sometimes treated
poorly in the theoretical literature also). Our (novel) solution here
is that selecting a negative literal which flounders does nothing to
the current goal. If a different literal is selected subsequently,
which would occur with a fair computation rule, failure may result; if
the same literal is always selected the tree will be infinite. If 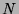 was considered a positive leaf in this case instead, and an exception
mechanism was invoked or some kind of abnormal termination was flagged
it could be more practical, but harder to formalise.
was considered a positive leaf in this case instead, and an exception
mechanism was invoked or some kind of abnormal termination was flagged
it could be more practical, but harder to formalise.
Figure 3:
Literal selection and floundering
 |
An advantage of our approach (at least in theory) is that it potentially
avoids a source of incompleteness. Suppose we have a goal with two ground
negated atoms, one of which flounders and the other succeeds. There is
no a priori way of determining which literal should be selected.
For example, in Figure , the goal 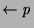 has a
successful SLDNF derivation but when the resolvent
has a
successful SLDNF derivation but when the resolvent
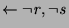 is encountered the right literal must be selected to avoid
floundering using the normal semantics. With our semantics we may first
select
is encountered the right literal must be selected to avoid
floundering using the normal semantics. With our semantics we may first
select 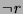 but that just leaves the current goal unchanged, allowing
us to then select
but that just leaves the current goal unchanged, allowing
us to then select 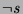 (a fair computation rule would select
(a fair computation rule would select 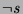 eventually; an unfair rule may result in a loop).
eventually; an unfair rule may result in a loop).



Next: Model-theoretic semantics
Up: A semantics for normal
Previous: A semantics for normal
2005-08-02
![]() is
is
![]() and the selected
literal is
and the selected
literal is ![]() , then
, then
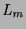 is an atom
is an atom 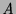 and
and
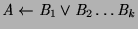 is a head instance of its definition, then
is a head instance of its definition, then 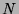 has
has 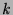 children,
connected with positive edges, with goals
children,
connected with positive edges, with goals
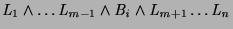 , for
, for
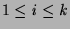 .
.
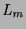 is a negative literal
is a negative literal 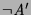 , there is one child
connected with a negative edge, containing goal
, there is one child
connected with a negative edge, containing goal 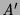 and the equality
atoms from
and the equality
atoms from 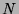 . If the subtree for
. If the subtree for 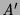 has a positive successful node
then
has a positive successful node
then 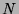 has a child, connected with a positive edge, which is failed.
If the subtree for
has a child, connected with a positive edge, which is failed.
If the subtree for 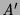 is finite and all positive leaves are failed,
then
is finite and all positive leaves are failed,
then 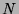 has a child, connected with a positive edge, which contains
has a child, connected with a positive edge, which contains
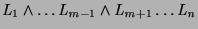 . If the subtree for
. If the subtree for 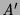 is finite, there are no positive successful nodes but there is a positive
floundered node, then
is finite, there are no positive successful nodes but there is a positive
floundered node, then 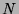 has a child, connected with a positive edge,
which is identical to
has a child, connected with a positive edge,
which is identical to 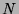 . Otherwise (the negative subtree is infinite
with no successful nodes),
. Otherwise (the negative subtree is infinite
with no successful nodes), 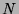 has no positive children and is considered
a positive leaf.
has no positive children and is considered
a positive leaf.
